Desestructurando el Puzzle de Einstein by Gheorghe Săsărman. Un homenaje a Flores para Algernon de Daniel Keyes.

¿Perteneces al 2% de la población que sabe resolver el acertijo de Albert Einstein?

El puzzle de la Cebra (1962) en el cuento "La evasión de Algernon" (1978) de Gheorghe Săsărman en su inteligente homenaje a Daniel Keyes por su "Flores para Algernon" (1958)

INTRODUCCIÓN:

Gheorghe Săsărman es un arquitecto rumano nacido en 1941 y residente en Alemania,

http://ro.wikipedia.org/wiki/Gheorghe_S%C4%83s%C4%83rman

La cuadratura del círculo (2001)

con una interesante obra de Ciencia Ficción y donde sólo se ham traducido al español dos de sus obras, su novela:

La Cuadratura del Círculo (2001). Publicada por Editorial La bibliotea del Laberinto en 2010. Editorial capitaneada por el incombustible Francisco Arellano.

La segunda obra traducida es el cuento “La evasión de Algernon” (1978) (título original “Evadera lui Algernon").

Esta brillante novela corta está publicada en el número 6, con fecha de marzo 2010, de la revista Delirio Ciencia Ficción y Fantasía, editada por la misma editorial: La biblioteca del  Laberinto. Por desgracia la página web de esta interesante editorial sigue en construcción.

El alcance de Gheorghe Săsărman en la ciencia ficción rumana es analizado por el traductor de ambas obras: Mariano Martín Rodríguez en su artículo:  "La fuga de Algernon" en la ciencia ficción rumana publicada como prefacio al cuento que nos ocupa.

El cuento de Săsărman explora una temática analizada por primera vez por Daniel Keyes en 1959 en su cuento Flores para Algernon y que en 1966 convirtió en nóvela con el mismo nombre (Flowers for Algernon). En palabras de Wikipedia su argumento es: 

http://es.wikipedia.org/wiki/Flores_para_algernon

La novela de 1966

"... Charlie Gordon es un chico de 32 años que sufre retraso mental con un cociente intelectual de 68. Es elegido para probar un tratamiento que podría triplicar su inteligencia mediante una operación. Sus progresos son comparados en paralelo con los de un ratón, Algernon, del cual el protagonista se hace amigo. Charlie nos cuenta, a través de sus informes de progresos, no sólo sus avances, sino también sus sentimientos y su propia evolución ascendente, lenta al principio, disparada hasta hacerle un genio después... y la caída cuando los mismos efectos del tratamiento le hacen perder todo lo ganado, sabiéndose que va a acabar tan mal como al principio, o peor. ..."

Charly (1968)

El cine ha realizado dos adaptaciones de esta novela al cine, en 1968, Charly que le valió un Oscar a Cliff Robertson y dirigida por Ralph Nelson y un telefilm para televisión (como su nombre índica) en el año 2000. En una adaptación bastante fiel a la novela, Cliff borda un papel de fácil lucimiento, transmitiendo la angustia que el nuevo Charlie Gordon sufre al conocer y hacerse evidente la reversión de su milagro.

Penny Marshall en 1990 llevó al cine la autobiografía del neurólogo norteamericano Oliver Sacks, en su inquietante Despertares (papel que le valió una nominación a Robert De Niro al interpretar al remedo de nuestro Charlie Gordon). La película narra el sorprendente descubrimiento, en 1969, de los efectos positivos de una droga sobre los catatónicos y su milagros despertar al mundo (de ahí el título), comparte con nuestra Charly, el gozo del despertar y la tragedia de la reversión. Al ser una obra basada en hechos reales renuncia explícitamente a cualquier tipo de especulación tan queridas por las obras de ciencia ficción, genero en el que se encuadran el resto de películas y textos que nos ocupa.

Despertares (1990) dirigida por Penny Marshall

El Cortador de Césped (1992) 

Pero el gran público, de conocer este tema, es por la película:

El cortador de Césped (1992) (The Lawnmower Man) dirigida por Brett Leonard  y donde Stephen King no tiene nada que ver con ella. Los guionistas son el propio Brett y Gimel Everett. Y cuyo argumento en palabras de filmaffinity es:

http://www.filmaffinity.com/es/film565150.html

"...  Un científico logra incrementar de forma extraordinaria la inteligencia de un deficiente mental mediante una combinación de drogas y realidad virtual. Pero el poder cerebral de este individuo pronto escapa al control del científico.   ..."

Con enfoques distintos ambas obras de ciencia ficción analizan la cuestión de acrecentar la capacidad intelectual de un ser humano y las consecuencias que tienen para él: sus motivaciones, sus sueños... Gheorghe Săsărman ataca la cuestión con una intención distinta: considera el incremento de las capacidades intelectuales como una infección y se pregunta sobre el efecto que tendrá sobre la sociedad, ¿Cómo trataran los infectados a los no infectados? ¿será el mundo igual?... algunas cuestiones las solventará y otras las dejará abiertas para que el lector alcance sus propias conclusiones.

Gheorghe Săsărman decide mostrar la sublime inteligencia alcanzada por su protagonista (el remedo de Charlie Gordon) tras el tratamiento/infección nada menos que resolviendo uno de los más famosos acertijos: el Puzzle de la Cebra, también conocido como el Acertijo de Einstein y aprovechar el impacto de la cantinela que siempre acompaña a las palabras Einstein's Puzzle: Sólo el 2% de la población es capaz de resolverlo. En descargo de Gheorghe, del traductor y del editor diré que no mencionan nada de todo esto en ningún momento, ni lugar.
El resto de esta entrada sigue con el enunciado de la versión Săsărman del acertijo extraído completamente del cuento. Luego sigue la elegante solución que Săsărman da en el cuento (también lo he extraído literalmente del cuento), revisito la solución aportando algunos gráficos y comentarios con la intención de verter luz en aquellos aspectos más oscuros. En la siguiente sección analizo y resuelvo el ramal de la bifurcación del acertijo, que el autor indica pero que no desarrolla. Posteriormente presento el acertijo original, destacando las diferencias con la versión Săsărman, reconvierto el puzzle original en una versión comparable con la versión de Săsărman. En la conclusión apunto las diferencias fundamentales en las soluciones de ambas versiones. En el anexo presento la solución al acertijo original con la técnica de resolución "a la Sudoku", también presento enlaces a blogs donde se publican otros métodos de solución al acertijo original.

EL ENUNCIADO

Extraído del cuento: 

“…La casa del inglés es roja. Suena bien el comienzo, me dije mirando la hoja de papel en la que se sucedían, una tras otras, las proposiciones concisas del test. …”

“…  los tests nunca me han atraído; los he evitado en el campo profesional y los he rechazado sin más como diversión. No los consideraba concluyentes y tampoco veía para qué me podría servir ocupar la mente con el único propósito de distraer a otros. Sin embargo esta vez tuve que ceder. El español tiene un perro. …”

“… El japonés es detective. …”

“… David solo me había advertido que se trataba de una prueba contra cronómetro, pero de todos modos tenía la sensación de que me perdía en ramificaciones tupidas e inútiles, que empezaba a extraviarme en el laberinto de mis propias ideas.  …”

“… El francés bebe té. …”

“… Me dijeron, claro, desde el principio, que se trataba de cinco casas de color distinto, unas al lado de otras, que sus propietarios tenían nacionalidades, profesiones y bebidas diferentes, además de tener junto a la casa un animal de especie distinta,  …”

“… La casa blanca está a la derecha de la casa verde. … “

“…los participantes formaban una especie de club, me pidieron, para dejarme entrar (sobre todo en broma, aunque también obedeciendo a una tradición), que resolviera el test en una hora como máximo, a lo que seguiría la concesión del diploma de miembro del club y la asignación de un rango que sería más alto según encontrara las respuestas con mayor rapidez. Tenía que especificar cuál de los cincos personajes bebía cerveza y cuál de ellos tenía una cebra.  …”

“… En la casa del medio se bebe leche. …”

Portada de Delirio 6

“… Y como las alegrías, igual que las desgracias, nunca vienen solas, ahora seguían dos frases no ambiguas: La casa del noruego es la primera de la izquierda. La casa vecina a la del noruego es azul. Mi paciencia había sido recompensada; me imaginaba las cinco casas y me decía que ya sabía algo definitivamente válido sobre las tres primeras: la primera era la del noruego, la siguiente era azul y en la tercera, la del medio se bebía leche. Les comuniqué a todos estas verdades como si fueran un triunfo personal, me ovacionaron, alguien observó que habrían transcurrido diez minutos, mientras que David añadió que apenas entonces empezaba lo difícil. ..:”

“… yo me concentraba en el test, en sus proposiciones claras, de una nitidez engañosa. La casa amarilla es del médico. El vecino del médico tiene un caballo. El vecino del inglés es arquitecto. El vecino del arquitecto tiene un zorro.  …”

Algernon

“… ¡Me había perdido completamente entre tanta casa, aunque solo eran cinco!

       Puede que las tres últimas premisas me lleven a resolver el enigma, me dije. El abogado bebe zumo de tomate. El ingeniero tiene un gato. En la casa verde se bebe café. En vano, ¡ni una explicación más! Al contrario, las tinieblas parecían volverse más densas: solo podía decir que el abogado no era francés (porque habría bebido te), que no vivía en la casa del medio (donde se bebía leche), como tampoco en la casa verde (donde se bebía café); que el ingeniero no era español (porque habría tenido un perro), o que la casa verde no podía ser de ningún modo la del medio (donde se bebía leche). Aquí la cabeza me daba vueltas y otra vez me dejé distraer… “

Esta ha sido la presentación de Săsărman, formalicemos un poco el acertijo que nos propone: 

1	La casa del inglés es roja
2	El español tiene un perro
3	El japonés es detective
4	El francés bebe té
5	La casa blanca está inmediatamente a la derecha de la casa verde
6	En la casa del medio se bebe leche
7	La casa del noruego es la primera de la izquierda
8	La casa vecina al noruego es azul
9	La casa amarilla es del médico
10	El vecino del médico tiene un caballo
11	El vecino del inglés es arquitecto
12	El vecino del arquitecto tiene un zorro
13	El abogado bebe zumo de tomate
14	El ingeniero tiene un gato
15	En la casa verde se bebe café
	¿quién bebe cerveza? ¿Quién tiene una cebra?

Nótese que en la quinta afirmación "ha aparecido" un inmediatamente que no está en el texto de la novela corta. Posteriormente explicaremos esta "aparición".

Presento la siguiente matriz, en la creencia que nos ayudará a visualizar mejor la solución. Es decir el acertijo consiste en rellenar esta tabla:

Cuadrícula a rellenar

Con la siguiente información, cada una en su casilla correcta:

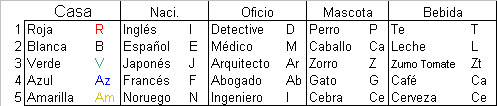Opciones posibles del acertijo

Ahora leamos la solución en palabras de Gheorghe Săsărman, pero antes: ... Apreciado lector, esta apunto de perder la oportunidad de intentar resolver este enigma por usted mismo, la elegancia de la solución sólo se puede disfrutar si se ha intentado resolver previamente.

LA SOLUCIÓN SĂSĂRMAN

Tras sufrir la infección del virus de la genialidad, nuestro protagonista...

“… De improviso, me volvió a la cabeza, como un sumergible empujado a la superficie de las aguas por una irresistible fuerza ascendente, el test de la víspera. La primera casa de la izquierda era la del noruego. La segunda era azul. En la del medio, la tercera, se bebía leche. Ahí me había quedado atascado. ¡Pero la continuación era evidente! La cuarta cara era verde, al ser aquella en que se bebía café; verde no podía ser ni la primera casa (pues a su derecha estaba una casa azul y no blanca, como se requería), ni la segunda casa (que era azul), ni la tercera (en la que se bebía leche y no café), ni siquiera la quinta (la cual, al ser la última, no tenía a su derecha ninguna otra casa), sino solo la cuarta casa. La quinta, al estar a la derecha de la verde, era blanca. Y una vez más resultaba sumamente sencillo seguir: como la casa del inglés era roja, solo podía ser la tercera, ya que la primera era la del noruego y las demás eran de otros colores. Por consiguiente, el noruego tenía que ser médico, porque la casa de médico era amarilla, y la única que podía tener color amarillo, por no haberlo deducido aún, era la primera casa, la del noruego. Por otro lado, el vecino del médico, es decir, el dueño de la segunda casa, el único vecino del noruego, tenía un caballo, mientras que el vecino del inglés era arquitecto. En este punto se bifurca la solución, al tener que elegir entre los dos vecinos del inglés. Me decidí por el dueño de la segunda casa, la azul, e hice bien. El abogado era, en consecuencia, el propietario de la quinta casa, porque bebía zumo de tomate; es verdad que sabía que el dueño de la primera casa era médico y el de la segunda, arquitecto; que en la tercera casa se bebía leche y en la cuarta, café. Estas dos condiciones, ser abogado y beber zumo de tomate, solo las podía reunir el dueño de la última casa. ¡Ahora todo se volvía más claro! El japonés era detective; solo quedaban dos casas con dueños de profesión desconocida: la tercera, de la que sabía que pertenecía la inglés, y la cuarta. Así pues, el japonés era el dueño de la cuarta casa. El español tenía un perro, y solo me quedaban dos casas cuyos dueños desconociera la  nacionalidad: la segunda, donde sabía que había un caballo, y la quinta. Pues bien, el español era el dueño de la última casa. El francés, bebía té y no podía ser otro sino el dueño de la segunda casa.

Gheorghe Săsărman

El ingeniero tenía un gato, y solo podía ser el dueño de la tercera casa. El vecino del arquitecto tenía un zorro; como de los dos vecinos, uno era ingeniero y tenía un gato, solo podía tener un zorro el otro, el médico, el dueño de la primera casa. En solo unos minutos había situado cada proposición en un contexto determinado, había determinado sin error la nacionalidad y la profesión de los cinco propietarios, el color de las cinco casas, los animales criados en cuatro de ellas y las bebidas preferidas en otras cuatro. Solo me quedaba dar respuesta a las dos preguntas finales y resolver el test. ¿Quién bebía cerveza? Evidentemente, el noruego, el dueño de la primera casa. Porque el francés bebía té, el inglés leche, el japonés café y el español zumo de tomate. ¿Quién tenía una cebra? Estaba claro que el japonés, el dueño de la cuarta casa. Porque el noruego tenía un zorro, el francés un caballo, el inglés un gato y el español un perro. Mis divagaciones de la noche anterior me parecían pueriles, todos los desvaríos que los demás veían graciosos me parecían desprovistos de sentido, cuando no estúpidos. Me daba cuenta de que también entonces había estado a punto de encontrar la clave del laberinto, pero mis ojos estaban como cegados por la niebla y no había acertado a zafarme de las redes de las asociaciones vacías de palabras, a evitar la trampa de las ramificaciones sin salida, de los bucles enrollados en sí mismos.  ..."

Ordeno la solución. El texto en cursiva es un añadido mío, cuyo objetivo es facilitar la comprensión de la solución.

 Săsărman. Tabla 1

1          La primera casa de la izquierda era del noruego.

2          La segunda era azul.

3          En la del medio, la tercera, se bebía leche.

4 y 5    La cuarta cara era verde, al ser aquella en que se bebía café;

 verde no podía ser ni la primera casa (pues a su derecha estaba una casa azul y no blanca, como se requería), ni la segunda casa (que era azul), ni la tercera (en la que se bebía leche y no café), ni siquiera la quinta (la cual, al ser la última, no tenía a su derecha ninguna otra casa), sino solo la cuarta casa.

6          La quinta, al estar a la derecha de la verde, era blanca.

Ahora es evidente la aparición del inmediatamente en la frase 5 del acertijo:

La casa blanca está inmediatamente a la derecha de la casa verde

Dado que la "inmediatez" se usa en la deducción 4, al descartar que la casa verde pudiera ser la primera casa y aunque Săsărman no la define explícitamente lo hace implícitamente al usarlo en su solución. Por eso he optado por presentar el enunciado del acertijo con el adverbio inmediatamente, a pesar que el autor no lo hace.

Săsărman. Tabla 2 Bifurcación

7 y 8    La casa del inglés era roja, solo podía ser la tercera,

ya que la primera era la del noruego y las demás eran de otros colores.

9 y 10  El noruego tenía que ser médico, porque la casa de médico era amarilla,

y la única que podía tener color amarillo, por no haberlo deducido aún, era la primera casa, la del noruego.

11        El vecino del noruego, tenía un caballo.

Por otro lado, el vecino del médico, es decir, el dueño de la segunda casa, el único vecino del noruego, tenía un caballo,

BIFURCACIÓN

El vecino del inglés era arquitecto. En este punto se bifurca la solución, al tener que elegir entre los dos vecinos del inglés. 

Posteriormente veremos que se podía haber deducido más información antes de plantear la bifurcación y probaré que efectivamente si el arquitecto viviera en la cuarta casa el acertijo no tiene solución.

Săsărman. Tabla 3

12        Arquitecto segunda casa.

Me decidí por el dueño de la segunda casa, la azul, e hice bien.

13 y 14  El abogado vive en la 5ª  casa y bebe zumo de tomate

El abogado era, en consecuencia, el propietario de la quinta casa, porque bebía zumo de tomate; es verdad que sabía que el dueño de la primera casa era médico y el de la segunda, arquitecto; que en la tercera casa se bebía leche y en la cuarta, café. Estas dos condiciones, ser abogado y beber zumo de tomate, solo las podía reunir el dueño de la última casa.

15 y 16            El japonés era detective, el japonés era el dueño de la cuarta casa.

Porque es la única casa donde se puede dar de forma simultánea.

Y ahora ya se puede entrar en la fase decisiva de las deducciones.

Săsărman. Tabla 4

17 y 18            El español tenía un perro,  el español era el dueño de la última casa.

Porque es la única casa donde se puede dar ambas cosas simultáneamente.

19 y 20            El francés, bebía té y no podía ser otro sino el dueño de la segunda casa.

21 y 22            El ingeniero tenía un gato, y solo podía ser el dueño de la tercera casa. 

Y las tes últimas deducciones:

Săsărman. Tabla 4 Solución

23        El médico tiene un zorro

El vecino del arquitecto tenía un zorro; como de los dos vecinos, uno era ingeniero y tenía un gato, solo podía tener un zorro el otro, el médico, el dueño de la primera casa.

24        ¿Quién bebía cerveza? Evidentemente, el noruego, el dueño de la primera casa. Porque el francés bebía té, el inglés leche, el japonés café y el español zumo de tomate.

25        ¿Quién tenía una cebra? Estaba claro que el japonés, el dueño de la cuarta casa. Porque el noruego tenía un zorro, el francés un caballo, el inglés un gato y el español un perro.

Elegante forma de resolverlo.

La forma que Gheorghe Săsărman se quita de en medio la bifurcación:
"... En este punto se bifurca la solución, al tener que elegir entre los dos vecinos del inglés. Me decidí por el dueño de la segunda casa, la azul, e hice bien. ..." 
requiere alguna explicación más... excepto si se es un genio, claro está.

LO QUE FALTA A LA SOLUCIÓN SĂSĂRMAN

Antes de resolver la rama de la bifurcación incongruente. Saquemos todo el partido posible a las 15 afirmaciones del acertijo, que sorprendentemente no hace Săsărman.
Haré la bifurcación lo más tarde posible en el camino que permite el acertijo, es decir obtendré el resto de deducciones que se puede obtener sin necesidad de suponer ninguna respuesta (tomar un ramal de una bifurcación):

Resolviendo Bifurcación Săsărman Tabla 1

1.- En la casa de en medio vive el ingeniero.
No puede ser detective ya que el detective es japonés y en la casa de en medio vive un inglés como ya sabemos.
El médico vive en la primera casa como ya sabemos.
No puede ser Arquitecto, porque el arquitecto es vecino del inglés. El inglés vive en la casa de en medio. Luego no puede ser vecino de si mismo.
No puede ser Abogado ya que el abogado bebe zumo de tomate y en la casa de en medio se bebe leche.
Sólo puede vivir el ingeniero.
2.- En la casa de en medio vive el gato. Ya que el ingeniero tiene un gato.
3.- En la primera casa se bebe cerveza.
No puede ser Té, porque el Té lo bebe el Francés y en la primera casa vive un noruego.
No puede ser leche, porque se bebe en la tercera casa. No puede ser café, porque se bebe en la cuarta casa. No puede Zumo de Tomate porque lo bebe el Abogado y en la primera casa vive un médico, no un abogado.
Ahora sí. Ahora estamos en la bifurcación. Pero dista mucho de ser la única existente. Es fácil ver que existen cuatro bifurcaciones posibles:

Resolviendo Bifurcación Săsărman Tabla 2

1.- Arquitecto a: (Propuesta de Săsărman)

a. Oficio, I2   y    b. Oficio, I4
Es equivalente a la bifurcación del Zorro a:
a. Mascota, I1    y    b. Mascota, I5.
2.- Español a:

a. Nacionalidad, I4   y   b. Nacionalidad, I5
Equivalente a Perro: a. Mascota, I4 y b. Mascota, I5.
3.- Francés a:

a. Nacionalidad, I2 y  b. Nacionalidad, I5.
Equivalente a Té: a. Bebida, I2 y b. Bebida, I5
4.- Abogado a:

a. Oficio, I2    y    b. Oficio, I5.
Equivalente a Zumo de tomate: a. Bebida, I2 y b. Bebida, I5.
El resto serían trifurcaciones, las centradas en el Japonés (equivalente a la centrada en el detective) y las centradas en la Cebra.

Ahora demostraré que escogiendo el otro ramal de la bifurcación llegamos a una incongruencia.

Resolviendo Bifurcación Săsărman Tabla 3

1.- El arquitecto vive en la cuarta casa. Por ser este el otro ramal de la bifurcación tomado por Săsărman.
2.- El zorro vive en la quinta casa. Como el zorro es vecino del arquitecto y en la casa tres vive el gato, el zorro sólo puede vivir en la quinta casa.
3.- La cebra vive en la primera casa. Sólo nos quedan dos animales; el perro y la cebra. El perro vive con el español. Como en la primera casa vive el noruego ahí no puede vivir el perro. Luego sólo puede vivir la cebra.
4.- El perro vive en la cuarta casa. No queda más casa sin mascota, que la cuarta.
5.- El español vive en la cuarta casa. Dado que el español tiene un perro y este vive en la cuarta casa.
Y por fin llegamos a la incongruencia (todas las incongruencias participan de este formato).

Nos quedan:
Dos nacionalidades; Japonés y Francés, dos oficios; Detective y Abogado y dos bebidas; Té y Zumo de Tomate.
Además sabemos que:
Identificado con ▲:                   el Japonés ( J ) es Detective ( D )
Identificado con ╬ :                   el Francés ( F ) bebe Té ( T )
Identificado con ♫:                    el abogado ( Ab ) bebe Zumo de Tomate ( Zt ).
Escojamos la casilla que escojamos, la elección que tomemos nos llevará a una incongruencia.
Supongamos que en la segunda casa vive el Japonés. Luego será detective. Pero ¿qué se bebe en la segunda casa? NADA. Dado que al no ser francés no se bebe Té y al no ser abogado no se bebe Zumo de Tomate.
Supongamos que en la segunda casa vive el Francés. Luego beberá Té. Pero ¿qué oficio tiene la segunda casa? NINGUNO. Por no ser japonés no es detective y por no beber zumo de tomate no es abogado.
Nótese que la paradoja es idéntica si en lugar de analizarla para la segunda casa se analiza para la quinta casa, e indistintamente se tome la nacionalidad, el oficio o la mascota.

ZEBRA PUZZLE.

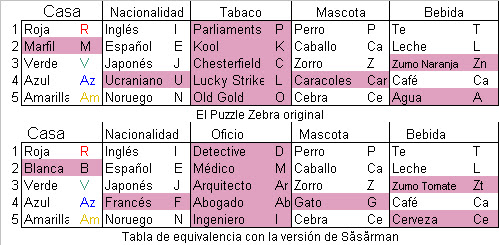
Este acertijo no ha sido creado por Gheorghe Săsărman. Erróneamente se le atribuye a Albert Einstein (Einstein's Puzzle o Einstein's Riddle) supuestamente siendo un niño habría creado este acertijo. Para hacerlo aún más llamativo se suele decir que Albert vaticinó que sólo el 2% de la población mundial podría resolver este acertijo. Sabemos que no lo creo Albert porque aún no existían las marcas de tabaco que aparecen en el acertijo original: el afamado Zebra Puzzle.

Fue publicado por primera vez el 17 de Diciembre de 1962 en Life International Magazine. Y la solución se publicó el 25 de Marzo de 1963.

En wikipedia se puede profundizar en este tema y encontrar varios métodos de resolución (todos ellos en inglés).
http://en.wikipedia.org/wiki/Zebra_Puzzle
En el anexo soluciono este acertijo y enlazo con blogs que también dan otros métodos de solución en español.

La 1ª publicación del Puzzle de la Cebra

El acertijo Cebra original:

1	Hay cinco casas
2	La casa del inglés es roja
3	El español tiene un perro
4	En la casa verde se bebe café
5	El Ucraniano bebe té
6	La casa verde está inmediatamente a la derecha de la casa Marfil
7	El fumador de Old Gold tiene caracoles
8	La casa amarilla fuman Kool
9	En la casa del medio se bebe leche
10	La casa del noruego es la primera casa
11	El fumador de Chesterfield es vecino del hombre que tiene un zorro
12	El vecino del caballo fuma Kools
13	El fumador de Lucky Strike bebe zumo de naranja
14	El japonés fuma Parliaments
15	La casa vecina al noruego es azul
	¿Quién bebe agua? ¿Quién tiene una cebra?

No hay oficios sino marcas comerciales de cigarrillos, ucraniano en lugar de francés... Adjunto la tabla de conversión del acertijo de la cebra original en los términos de la versión del acertijo propuesta por Săsărman :

Expreso el puzzle original en términos de la versión de Săsărman:

1	La casa del inglés es roja
2	El español tiene un perro
3	El japonés es detective
4	El francés bebe té
5	La casa verde está inmediatamente a la derecha de la casa blanca
6	En la casa del medio se bebe leche
7	La casa del noruego es la primera de la izquierda
8	La casa vecina al noruego es azul
9	La casa amarilla vive el médico
10	El vecino del médico tiene un caballo
11
12	El vecino del arquitecto tiene un zorro
13	El abogado bebe zumo de tomate
14	El ingeniero tiene un gato
15	En la casa verde se bebe café
	¿quién bebe Cerveza? ¿Quién tiene una cebra?

Nótese la existencia de tres variaciones sustanciales:

A.- Eliminación de la afirmación de la existencia de las 5 casas, por no aportar nada.

B.- La afirmación 5 invierte el orden de la versión de Săsărman. Sorprendentemente esta es la variación fundamental de las tres. Tanto es así, que en la solución al puzzle original se requiere resolver dos bifurcaciones. Mientras que en la versión Săsărman sólo se requiere resolver una bifurcación. Obviamente una bifurcación adicional complica la resolución de forma exponencial y complica una solución literaria tan elegante como la que Săsărman nos ha regalado.

C.- En compensación por la eliminación de la primera afirmación del caso original (las cinco casas) en la versión Săsărman se añade una afirmación adicional; la 11.-  El vecino del inglés es arquitecto. Completando el carácter sorprendente de las tres variaciones, esta afirmación es REDUNDANTE.... lo cual significa que no es necesaria para la resolución, pero simplifica mucho la solución. 

En el Anexo resuelvo el acertijo original en términos de la versión Săsărman por el método deductivo "a la Sudoku".

CONCLUSIÓN

Săsărman para ilustrar la genialidad de su personaje (una vez debidamente infectado por el gen de la genialidad) usa el conocido acertijo de la Cebra, falsamente atribuido a Albert Einstein. 
Es más que evidente la elegancia de su resolución en "La evasión de Algernon" alcanzando el objetivo que se marcó al incluir este acertijo en su cuento.
Sin embargo también cabe comentar tres elementos que sustentan el éxito y elegancia de la demostración Săsărman :

1.- Añade una afirmación adicional  en el acertijo, redundante eso sí, pero que simplifica la resolución.

2.- Altera el orden de las casas blanca y verde en la quinta afirmación del acertijo original, lo que le permite evitar una segunda bifurcación en la solución.

3.- Nos ahorra la prueba de que el camino alternativo (de la bifurcación) nos lleva a una incongruencia. Para mayor desgracia esta bifurcación no es única... 

Sin embargo, no debemos perder de vista que estamos ante un brillante uso literario de unos de los acertijos mentales más afamados.

ANEXO

Solución (simplificada) del acertijo original, expresado en los términos de la versión utilizada por Gheorghe Săsărman.

Lo primero que debe señalarse es que la solución que obtendré diferirá de la solución de Săsărman  en que la casa 4 y 5 intercambian posiciones (para ver solución de Săsărman ver la tabla 4).

La doble bifurcación que requiere la resolución implicaría la exploración de todas y cada una de las ramas que se plantean: 12 únicamente considerando las bifurcaciones y dejando de lado las trifurcaciones y cuatrifurcarciones de la primera encrucijada. Ciertamente muchas de esas singladuras acaban convergiendo a caminos ya explorados por alguna alternativa anterior. Sin embargo no es el propósito de esta artículo completarlo, por lo que nos centraremos en un único camino exitoso que ilustre el método de resolución "más lento pero seguro", de las mentes no afectadas por el virus de la genialidad.
Es fácil encontrar, en español, otras soluciones más rápidas:

http://innovacioneducativa.upm.es/pensamientomatematico/node/43

http://www.juegosdelogica.com/solucion_acertijo_de_einstein.htm

A continuación muestro la tabla de partida con todas las opciones posibles y donde los caracteres representan las opciones indicadas en la tabla de convergencia entre ambas versiones del acertijo.

Punto de Partida. Gráfico 0

A partir de ese punto voy a ir deduciendo las restricciones que las afirmaciones del acertijo original en términos de Săsărman nos impone. Para ello será necesario que complementemos las iniciales de las opciones con iconos que pretendidamente simplifiquen la resolución:

Zebra. Gráfico 1

1.- La casa del inglés es roja

Inglés ↔ Roja.  Marcamos I y R con un ●

De tal forma que cuando en una casa no puede ser del inglés tampoco será roja.

Y cuando sea del inglés será roja y al revés.

2.- El español tiene un perro

Español ↔ Perro. Marcamos E y P con un ■.

3.- El japonés es detective.

Japonés ↔ Detective. Marcamos J y D con un ▲

4.- El francés bebe té.

Francés ↔ Té. Marcamos F y T con un ╬.

5.- La casa verde está inmediatamente a la derecha de la casa blanca.

Luego la I1 (primera casa) no puede ser la casa Verde ni la última (I5) Blanca

Borro, V de Casa, I1 y borro, B de Casa, I5

6.- En la casa del médico se bebe leche.

Bebida, I3 = Leche

Fila Bebida borramos todas la L

Por beberse leche no se bebe Te y por ╬ borro francés en Nacionalidad, I3

Zebra .Gráfico 2

7.- La casa del noruego es la primera de la izquierda.

Nacionalidad, I1 = Noruego

Fila Nacionalidad borramos todas la N.

Por no ser Inglés y por ● borramos R en Casa, I1.

Por no ser Español y por ■ borramos Perro en Mascota, I1.

Por no ser Japonés y por ▲ borramos Detective en Oficio, I1

Por no ser Francés y por ╬  borramos Té en Bebida, I1

8.- La casa vecina al noruego es azul

Casa, I2 = Azul

Fila Casa borramos todas la Az.

Por no ser Roja y por ● borramos I en Nacionalidad, I2

Por no ser Blanca y por el enunciado 5, la casa I3 no puede ser Verde borramos Verde en Casa, I3.

Por no ser Verde y por el enunciado 5, la casa I1 no puede ser Blanca borramos Blanca en Casa, I1.

1º ¡¡ Hallazgo !!    Casa, I1 sólo puede ser Amarilla Am. Casa, I1 = Amarilla.

Fila Casa borramos todas las Am

Aquí podríamos deducir que Casa, I4 no puede ser Roja. Pero no lo tendremos en cuenta, por ahora.

Zebra. Gráfico 4

9.- La casa amarilla es del médico. Oficio, I1 = Médico.

Fila Oficios borramos Médico.

10.- El vecino del médico tiene un caballo. Mascota, I2 = Caballo.

Fila Mascotas borramos Caballo.

Por no ser Perro y por ■  borramos Español de Nacionalidad, I2.

11.- NO HAY AFIRMACIÓN 11.

12.- El vecino del arquitecto tiene un zorro.

Así Arquitecto y Zorro deben estar en casillas contiguas lo que indicamos con:

Ar vZ    y    Z vAr

13.- El abogado bebe zumo de tomate.

Abogado ↔ Zumo de Tomate.  Marcamos Ab y Zt con un ♫.

El médico, al no ser abogado, no bebe Zumo de tomate. Borramos Zt casilla Bebida, I1

En la casa I3, beben leche, luego no puede ser abogado. Borramos Ab en Casilla Oficio, I3

Zebra. Gráfico 5

14.- El ingeniero tiene un gato.

Ingeniero ↔ Gato. Marcamos I y G con un ☼.

El médico no tiene gato, borramos G Casilla Mascota, I1

La casa 2 por tener un caballo no será ingeniero, borramos I Casilla Oficio, I2.

15.- En la casa verde se bebe café.

Verde ↔ Café. Marcamos V y Ca con un ♥.

La casa I1 y I2 no son verdes, luego no beben café. Nótese que en la casa I3 beben leche, luego no puede ser verde, pero ya sabiamos que Casa, I3 no era verde. Borramos Ca en Bebida, I1 y Bebida, I2

2º ¡¡ Hallazgo !!    Bebida, I1 sólo puede ser Cerveza. Bebida, I1 = Cerveza.

Fila Bebida borramos todas la Ce

   Y acabamos las afirmaciones y con ellas las deducciones. Estamos en una encrucijada lo que Săsărman llamó bifurcación.... sin embargo no hay una única bifurcación... hay 5, aunque realmente distintas hay 4.

Zebra. Gráfico 5: 1ª Bifurcación

1.- Casilla Mascota, I1

a. Zorro   y    b. Cebra

2.- Casilla Nacionalidad, I2

a. Japonés   y   b. Francés

3.- Casilla Bebida, I2

a. Té    y   b. Zumo de tomate

4.- Casilla Casa, I3

a. Roja    y    b. Verde

que es equivalente a Casilla Casa, I5; a. Roja   y   b. Verde

El resto serían trifurcaciones o peor...

En este momento es evidente que el cambio de orden de la afirmación 5, de las casas blanca y verde lastra la solución. Ya que con el orden de Săsărman (es decir la casa Verde sólo podría estar en I3 e I4) y dado que en la casa I3 se bebe leche, sería inmediato deducir que la casa I4 es verde, que se bebe café.... que la casa roja es I3, donde vive el inglés....
Pero no es el caso. Ya comenté que una demostración completa requeriría seguir todos los posibles caminos y verificar que llevan a la única solución o a una incongruencia. Pero no lo haré por ser una tarea hercúlea y alejado del objetivo de esta entrada. Seguiré la primera bifurcación; la opción a:

Zebra. Gráfico 6

Casilla Mascota, I1 = Zorro

Borramos Z en fila Mascotas

Por ser Zorro y por vZ su vecino es arquitecto. Casilla Oficio; I2 = Arquitecto

Borramos Arquitecto en fila Oficios

Por no ser detective y por ▲, no es japonés. Borramos J de Casilla Nacionalidad, I2

1º ¡¡ Hallazgo!! La casilla Nacionalidad, I2 sólo puede ser Francés. Analizo luego.

Por no ser Abogado y por ♫, no bebe Zumo de Tomate. Borramos Zt de Casilla Bebida, I2

2º ¡¡ Hallazgo!! La casilla Bebida, I2 sólo puede ser Te. Analizo luego.

Análisis 1º Hallazgo. Casilla Nacionalidad, I2 = Francés

Borramos Francés de la fila de Nacionalidades.

Por ser Francés y por ╬ se vuelve a deducir el 2º Hallazgo.

Análisis 2º Hallazgo. Casilla Bebida, I2 = Te

Borramos Té de la fila de Bebidas

No se pueden realizar más deducciones. Estamos antes la segunda bifurcación.

Zebra 7. 2ª Bifurcación

Nueva encrucijada. Posibles bifurcaciones:

1.- Casilla Casa, I3

a. Roja   y   b. Blanca

Que es equivalente a Casa, I5: a Roja   y   b. Verde

2.-  Casilla Oficio, I3

a. Detective   y   b. Ingeniero

3.- Casilla Bebida, I4

a. Zumo de tomate   y    b. Café

que es equivalente a Bebida, I5: a. Zt   y   b. Ca

El resto son trifurcaciones.

Tomamos de nuevo la primera bifurcación que nos encontramos; opción a:

Zebra 8

Casilla Casa, I3 = Roja

Borramos Roja de la fila de Casa

1º ¡¡ Hallazgo!! La casilla Casa, I4 sólo puede ser Blanca. Analizo luego.

2º ¡¡ Hallazgo!! La casilla Casa, I5 sólo puede ser Verde. Analizo luego.

Por ser Roja y por ● , es Inglés. Casilla Nacionalidad, I3 = Inglés

Borramos Inglés de la fila de Nacionalidades

Por no ser Español y por ■ no tiene perro. Borramos perro de la casilla Mascota, I3

Por no ser Japonés y por ▲  no es detective. Borramos detective de Oficio, I3

3º ¡¡ Hallazgo!! La casilla Oficio, I3 sólo puede ser Ingeniero

Casilla Oficio I3 = Ingeniero

Borramos Ingeniero de la final de Oficios

Por ser Ingeniero y por ☼ , tiene un Gato.  Casilla Mascota, I3 = Gato

Borramos Gato de la fila de Mascotas

Cierro el análisis con la últimas deducciones:

Zebra 9

Análisis 1º Hallazgo. Casa, I4 = Blanca

Nótese que no tiene consecuencias más allá de volver a encontrar el 2º Hallazgo

Análisis 2º Hallazgo. Casa, I4 = Verde. 

Por ser verde y por ♥ bebe café. Bebida, I5 = Café

Borramos Café de la fila de bebida

La casilla Bebida, I4 sólo puede ser Zumo de tomate; Bebida, I4 = Zumo de Tomate

Por ser Zumo de Tomate y por ♫ , I4 es Abogado. Oficio, I4 = Abogado

Borramos Abogado de la fila de Oficios

La casilla Oficio I5 sólo pueda ser Detective. Oficio, I5 = Detective

Por ser Detective y por ▲ I5 es Japonés.  Nacionalidad, I5 = Japonés

Borramos Japonés de la fila de Nacionalidades

La casilla Nacionalidad I4 sólo pueda ser Español: Nacionalidad, I4 = Español

Por ser Español y por ■, I4 tiene un Pero: Mascota, I4 = Perro

Borramos Perro de la fila de Mascotas

La casilla Mascota, I5 sólo pueda ser Cebra: Mascota, I5 = Cebra.

Cerrando el Acertijo

I1 bebe Cerveza e I5 tiene una Cebra. 

Zebra 10: solución

Como ya había anticipado las soluciones de las casas 4 y 5 han intercambiado sus posiciones como fácilmente se puede comprobar al comparar esta tabla con  Săsărman Tabla 4. Solución.